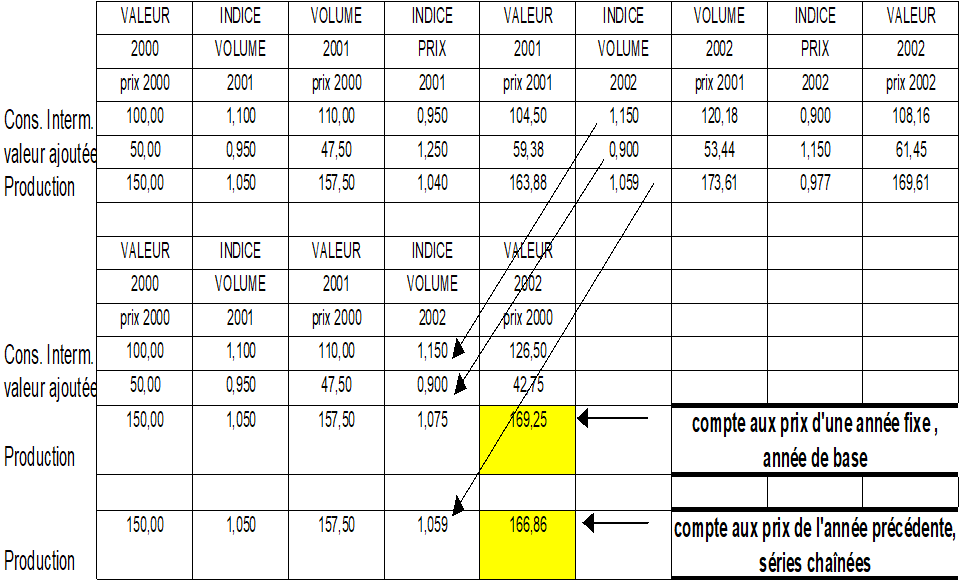
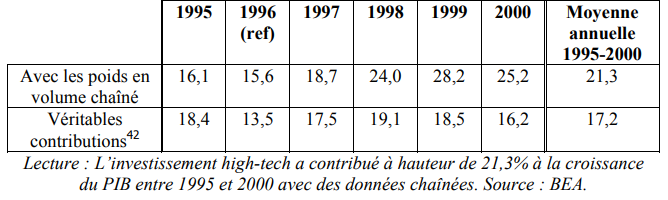
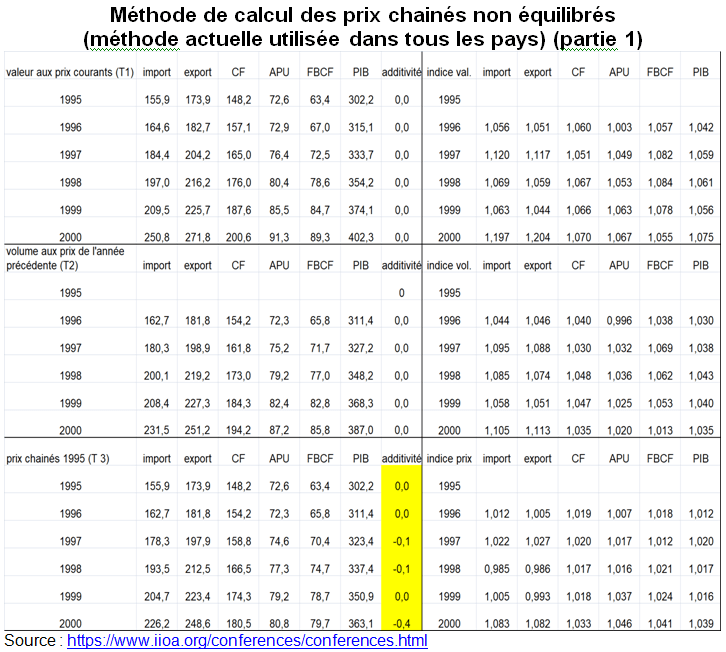
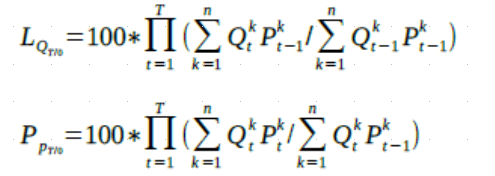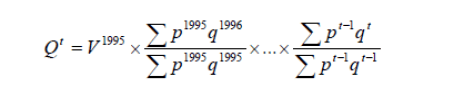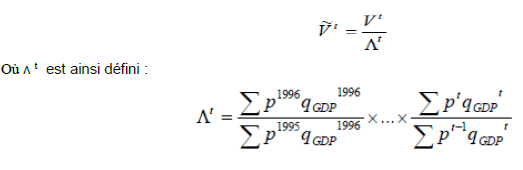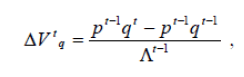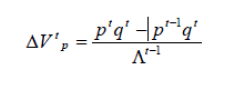- Les comptes annuels à prix constants (on dit aussi «en volume») depuis la base 2000 sont publiés «en prix chaînés, année de base, non additifs». A cet effet les évolutions des données aux prix de l’année précédente sont chaînées pour construire des séries d’évolutions sur longue période, dont chaque élément annuel est l’évolution de l’agrégat aux prix de l’année précédente. Le chaînage s’effectue à chaque niveau du TES. Aucun équilibrage n’est effectué, de sorte que les prix ne sont pas modifiés [7].
- Les problèmes spécifiques au chaînage des variations de stocks ont conduit à construire une méthode adaptée, appliquée à chaque type de variations de stocks : cette méthode cherche à respecter les contributions des variations de stocks à la croissance du PIB. C’est donc la «variation de variations de stocks» (écart entre les variations de stocks de l’année n et de l’année n-1, estimés dans un même système de prix, celui de l’année n-1) qui est la variable privilégiée, et qu’on évite de distordre par le passage aux prix chaînés ; celle-ci est déflatée par un indice adapté à la nature des stocks pour tenir compte de l’évolution des prix entre l’année de référence et l’année n-1. On calcule ensuite la variation de stocks aux prix chaînés par chaînage additif pour chaque composante, et la variation totale comme la somme de ses trois composantes.
Formules de calcul
2/ Applications
a) Méthode
Le point de départ est la série chronologique constituée par la croissance au prix de l’année précédente.
On » relie » ensuite ces taux de croissance.
On obtient un indice base 100 à une année arbitraire donnée (par exemple l’année de base 2010 en France).
On multiplie ensuite cet indice par le montant au prix courant de cette année arbitraire.
Cette dernière étape n’affecte en rien la dynamique de la série temporelle, elle permet seulement de la montrer » en niveau « .
Cela donne en France des » Comptes aux prix de l’année précédente, chaînés, base 2010 » mais d’autres noms sont parfois utilisés : » euros chaînés « , » prix chaînés « .
b) Pratiques en France
Les comptes annuels sont établis au niveau » H 327 « .
On part des comptes en prix courants de l’année précédente
On applique des indices de quantité
On obtient des comptes additifs à prix constants de l’année précédente.
On additionne ces comptes au niveau G (138), au niveau F (38), au niveau E (16) …jusqu’au niveau 1 (économie globale)
On calcule les taux de croissance pour tous les agrégats
On relie ces taux de croissance
On multiplie par le montant à prix courant de l’année de base 2010 pour chaque agrégat.
IV – UN EXEMPLE DE L’INTÉRÊT DU CALCUL DES PRIX CHAÎNÉS
1/ L’évolution du PIB dans l’EU-27: croissance depuis 2014
La crise économique et financière mondiale a entraîné une grave récession dans l’EU-27 en 2009 (voir graphique 1), suivie d’une reprise en 2010. La crise avait éclaté plus tôt au Japon et aux États-Unis, où des taux de variation annuels négatifs du PIB (en termes réels) avaient déjà été enregistrés en 2008, s’étaient détériorés en 2009, avant de connaître un rebond en 2010. À l’inverse, la production économique chinoise (Hong Kong compris) a continué de croître à un rythme soutenu pendant la crise (près de 10 % par an), avant de ralentir quelque peu au cours des années suivantes, tout en demeurant sensiblement plus élevée que dans les autres économies représentées dans le graphique suivant.
La crise était déjà manifeste dans l’UE-27 en 2008, puisque le taux de croissance du PIB avait accusé une baisse considérable, qui a été suivie par une chute du PIB réel de 4,3 % en 2009. La reprise dans l’EU-27 a vu l’indice de volume du PIB (indice chaîné) augmenter de 2,2 % en 2010 et de 1,8 % en 2011. Par la suite, le PIB s’est contracté de 0,7 % en 2012 et l’évolution a été négligeable en 2013, avant qu’un taux de variation positif ne soit enregistré en 2014 (1,6 %). Entre 2015 et 2018, la croissance a adopté un rythme relativement stable de 2,0 % à 2,8 % par an. En 2019, la croissance a ralenti et l’EU-27 a enregistré une augmentation réelle du PIB de 1,5 %.
Dans la zone Euro, les taux de variation correspondants étaient semblables à ceux de l’EU-27: les contractions enregistrées en 2009 et 2012 ont été plus fortes (-4,5 % et -0,9 %) que dans l’EU-27 et la contraction de 2012 s’est poursuivie jusqu’en 2013 (-0,2 %), tandis que la situation est restée inchangée dans l’EU-27 en 2013. Si une augmentation a été enregistrée dans la zone euro au cours de chaque année lors de laquelle une augmentation a été enregistrée dans l’EU-27, le taux de croissance dans la zone euro était cependant normalement 0,1 ou 0,2 point de pourcentage inférieur. En conséquence, au cours de la période 2009-2019, la croissance du PIB réel dans la zone euro a été légèrement inférieure à celle de l’EU-27 dans son ensemble.
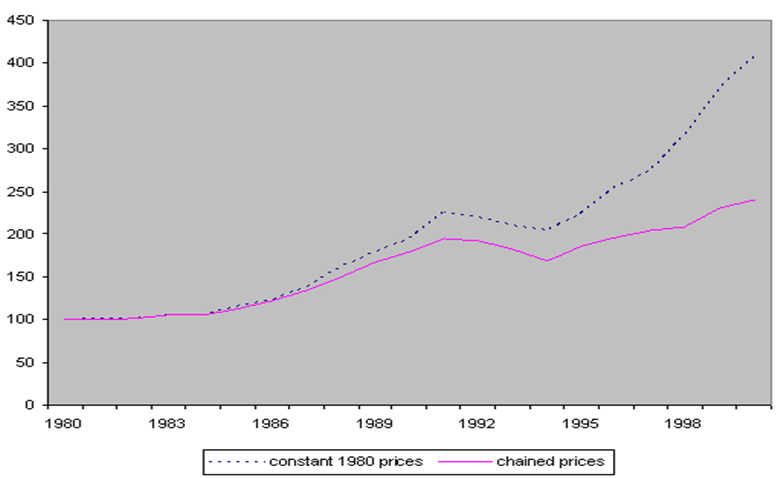
Évolution du PIB réel, 2009-2019 (en % de variation en glissement annuel)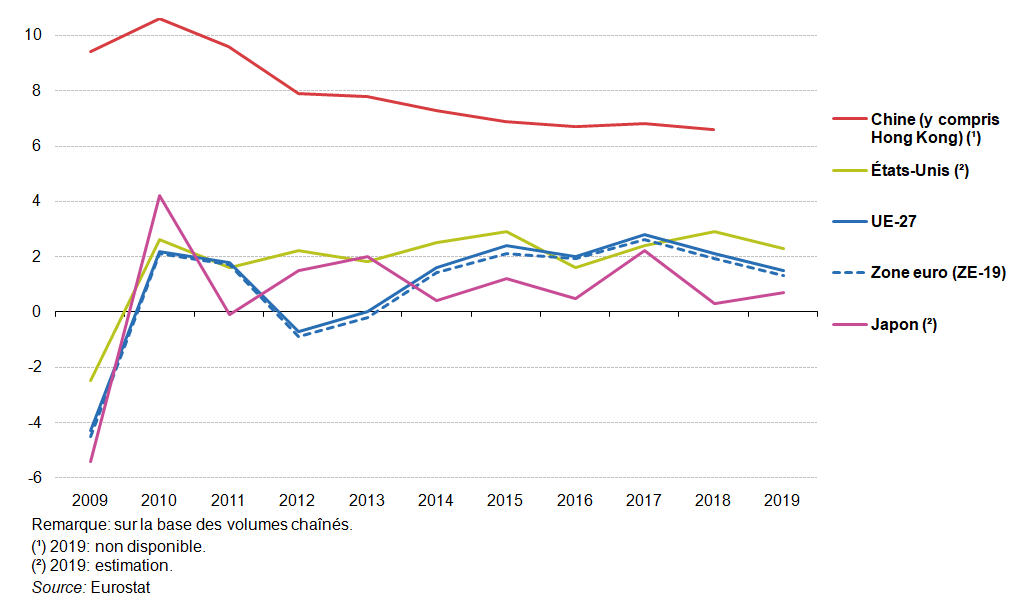
2/ Évolution différente des activités économiques au cours de la dernière décennie
Entre 2009 et 2014, la production de l’agriculture, de la sylviculture et de la pêche dans l’EU-27 a fluctué, avec des taux de variation compris entre – 4,7 % et 5,4 % Les évolutions ont ensuite été plus modérées, avec des diminutions de 0,7 % et 1,1 % en 2015 et 2016, suivies par trois hausses relativement faibles (0,4 %-1,3 %) entre 2017 et 2019. Au total, la production a été 5,0 % plus élevée en 2019 qu’en 2009. La production industrielle de l’EU-27 a augmenté de 11,9 % entre 2009 et 2011, connaissant un rebond après la crise, mais a diminué de 2,3 % entre 2011 et 2013. Celle-ci a ensuite crû à un rythme relativement rapide au cours des quatre années qui ont suivi (avec des augmentations annuelles comprises entre 2,4 % et 3,3 %) et plus modéré (1,9 %) en 2018 avant de connaître une diminution de 0,5 % en 2019. La production industrielle a été 24,5 % plus élevée en 2019 qu’en 2009. La construction a connu la contraction la plus longue et la plus importante, caractérisée par un recul de la production de 14,9 % entre 2009 et 2013 pour l’EU-27 (elle était déjà en baisse en 2008 et 2009), chaque année enregistrant un nouveau recul. À ce titre, l’augmentation de 1,6 % enregistrée en 2015 (après une absence d’évolution en 2014) pour la construction a marqué la première croissance annuelle du secteur en huit ans et a été suivie d’une croissance de 1,3 % à 3,8 % jusqu’en 2019. En dépit de cette récente période de croissance soutenue, la production de la construction en 2019 a été 3,4 % plus faible qu’en 2009 (et donc considérablement plus faible qu’avant le début de la crise).
Deux activités de services (l’information et la communication et les activités immobilières) ont enregistré des taux annuels de variation positifs chaque année entre 2009 et 2019. Une situation similaire a été observée pour les services aux entreprises, à l’exception d’une légère baisse de 0,2 % en 2012, pour l’administration publique, l’enseignement, la santé humaine et l’action sociale, à l’exception d’un statu quo en 2012 et d’une légère baisse de 0,1 % en 2013, et pour le commerce, le transport, l’hébergement et les activités de restauration, à l’exception d’une baisse de 0,5 % en 2013. Parmi ces activités, la croissance totale la plus rapide entre 2009 et 2019 a été enregistrée pour l’information et la communication, avec une production 48,9 % plus élevée en 2019 qu’en 2009; la croissance la plus lente a été enregistrée pour l’administration publique, la défense, l’enseignement, la santé humaine et l’action sociale (+ 9,5 % au total). Les deux activités de services restantes (les activités financières et d’assurance ainsi que les arts, les spectacles, les activités récréatives et les autres activités de service) ont connu trois années de baisse de la productivité entre 2009 et 2019 et une croissance globale relativement modérée de respectivement 5,4 % et 4,8 %.
En 2019, toutes les activités de l’EU-27 ont enregistré une croissance de leur valeur ajoutée brute par rapport à 2018, à l’exception de l’industrie. Les activités affichant la croissance la plus forte ont été les activités d’information et de communication (3,9 %) et la construction (3,4 %). La production industrielle a diminué de 0,5 %, tandis que la croissance la plus lente parmi les autres activités a été observée dans l’agriculture, la sylviculture et la pêche (0,4 %).
Évolution réel de la valeur ajoutée brute, UE-27, 2009-2019 (2010 = 100)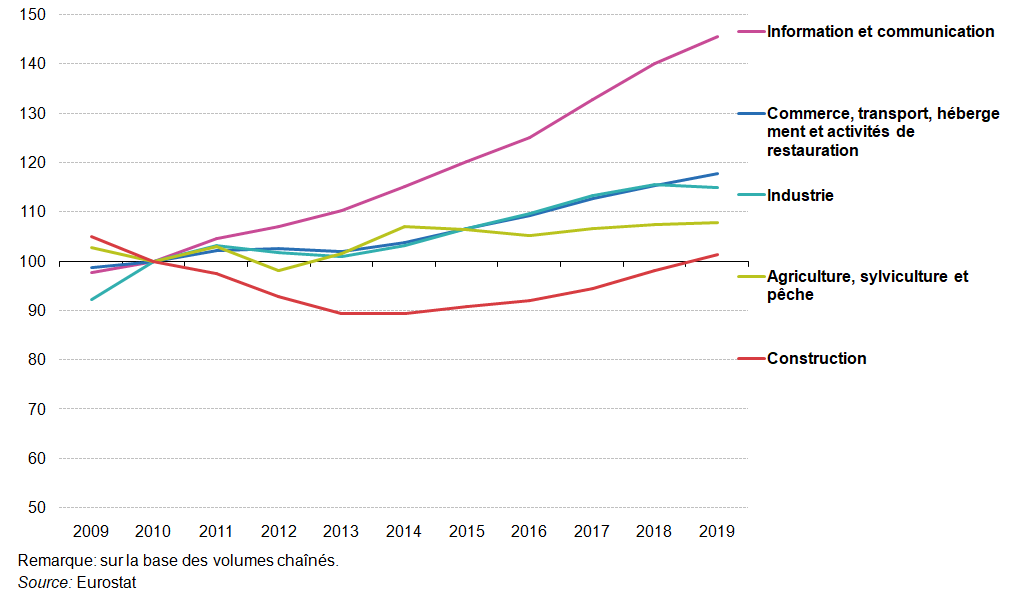
Évolution réel de la valeur ajoutée brute, UE-27, 2009-2019, (2010 = 100)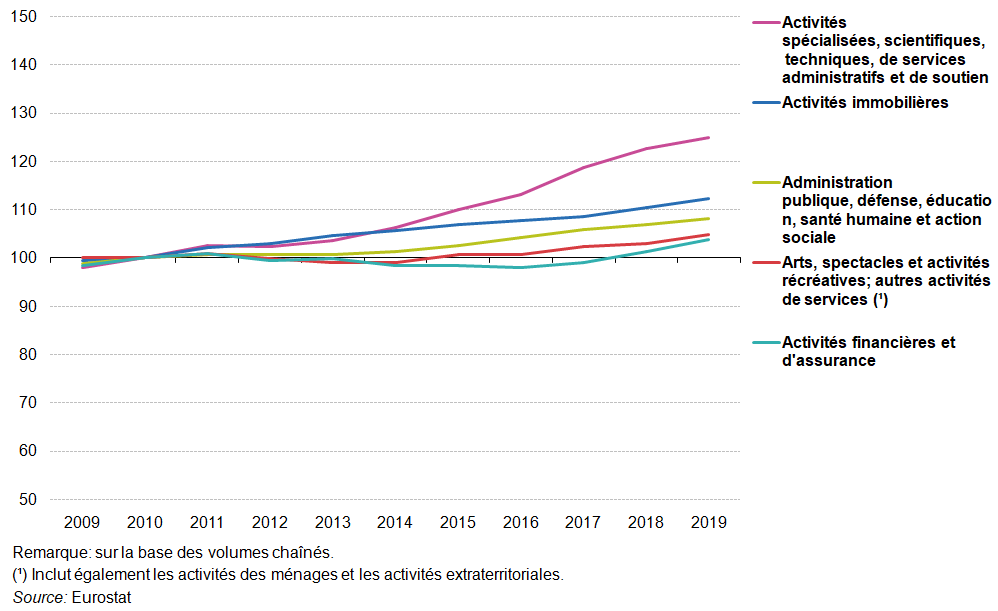
3/ La productivité de la main-d’œuvre
Afin d’éliminer les effets de l’inflation, on peut calculer la productivité du travail par personne occupée à l’aide de données corrigées des variations de prix. L’analyse de la productivité de la main-d’œuvre par personne occupée en termes réels (sur la base des volumes chaînés) au cours de la même période de dix ans (de 2009 à 2019) révèle une hausse pour la plupart des activités dans l’EU-27: les gains de productivité les plus importants ont été enregistrés pour l’agriculture, la sylviculture et la pêche (hausse globale de 30,1 %), l’industrie (24,3 %) et les services d’information et communication (22,8 %) (graphique suivant).
Il est à noter qu’une comparaison précise en termes réels des niveaux de productivité de la main-d’œuvre entre les activités ne peut être analysée que pour l’année de référence 2010 en raison de la non-additivité des volumes chaînés.
Productivité réelle de la main-d’œuvre, UE-27, 2009, 2014 et 2019, (en milliers d’euros par personne occupée)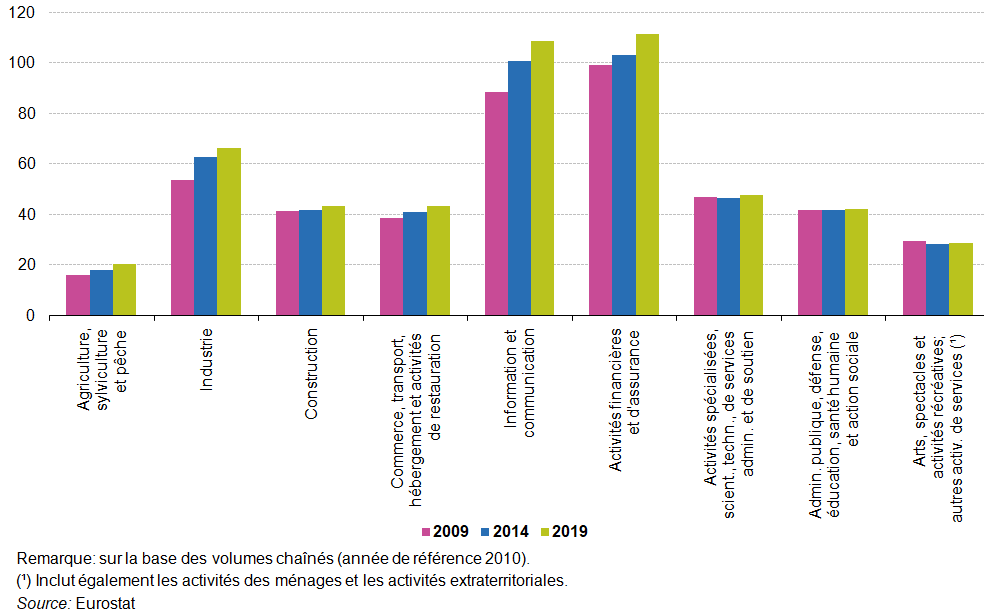
Le tableau suivant présente d’autres données sur l’évolution de la productivité réelle de la main-d’œuvre mesurée soit par personne occupée, soit par heure travaillée. Entre 2009 et 2019, la productivité de la main-d’œuvre par personne occupée a augmenté en termes réels dans la quasi-totalité des États membres de l’EU-27, le seul pays ayant enregistré un recul étant la Grèce (aucune donnée disponible pour Malte). De même, au cours de la même période, la productivité de la main-d’œuvre par heure travaillée a aussi progressé dans tous les États membres de l’EU-27, à l’exception la Grèce (aucune donnée disponible pour Malte). Les plus fortes (en pourcentage) pour les deux mesures de la productivité réelle de la main-d’œuvre ont été enregistrées en Roumanie, en Bulgarie, en Estonie et en Lettonie, et les plus faibles (en dehors de la Grèce) au Luxembourg et en Italie.
Productivité réelle de la main-d’œuvre, 2009, 2014 et 2019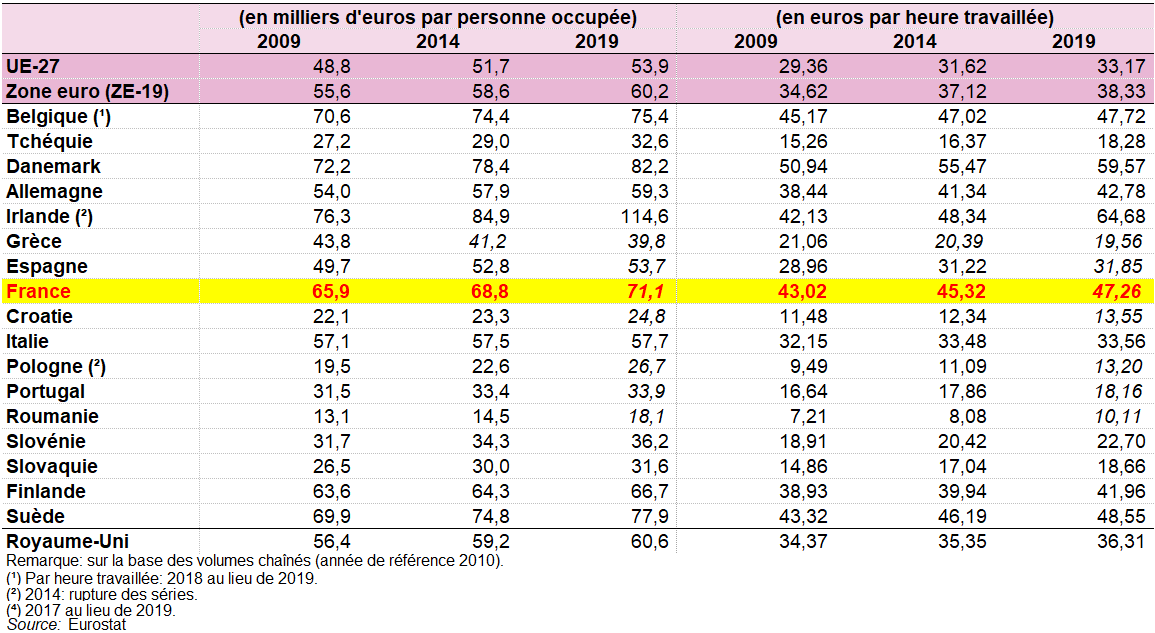
4/ Les dépenses de consommation et d’investissement
Si on analyse l’évolution des composantes du PIB du point de vue des dépenses, on peut remarquer que le volume des dépenses de consommation finale dans l’EU-27 a augmenté de 10,8 % entre 2009 et 2019 (graphique suivant), malgré une légère diminution en 2012 et en 2013. Les dépenses de consommation finale des administrations publiques ont progressé un peu plus lentement, de 10,0 % entre 2009 et 2019. Au cours de la même période, la formation brute de capital a été relativement volatile: elle a augmenté de 8,2 % entre 2009 et 2011, a diminué presque dans la même proportion (8,1 %) entre 2011 et 2013, et a ensuite suivi une tendance à la hausse jusqu’à 2019, avec une augmentation de 26,9 % entre 2013 et 2019. La croissance des exportations a dépassé celle des importations entre 2009 et 2013, ainsi qu’en 2017, tandis que les importations ont augmenté plus rapidement au cours des cinq des six années comprises entre 2014 et 2019. Entre 2009 et 2019, les exportations ont globalement augmenté de 61,0 % tandis que les importations ont augmenté de 55,3 %.
Après avoir reculé en 2009, les dépenses de consommation des ménages et des ISBLSM ont affiché une hausse en 2010 (de 0,9 % en volume) ainsi qu’en 2011 (+ 0,3 %), avant de marquer un nouveau recul en 2012 (- 0,9 %) et en 2013 (- 0,5 %). Ces dépenses ont ensuite augmenté pendant six années consécutives, avec une croissance passant d’abord de 1,1 % à 2,2 %, avant de revenir à 1,6 % en 2019.
En 2010, la croissance des dépenses totales es APU de l’EU-27 a ralenti en volume, puis est restée relativement stable (entre – 0,2 % et 0,4 %) entre 2011 et 2013, avant de s’inverser pour afficher une croissance un peu plus forte entre 2014 et 2019 (de 1,0 % à 2,0 %).
Évolution réel des dépenses de consommation, formation brute de capital, exportations et importations, UE-27, 2009-2019, (2010 = 100)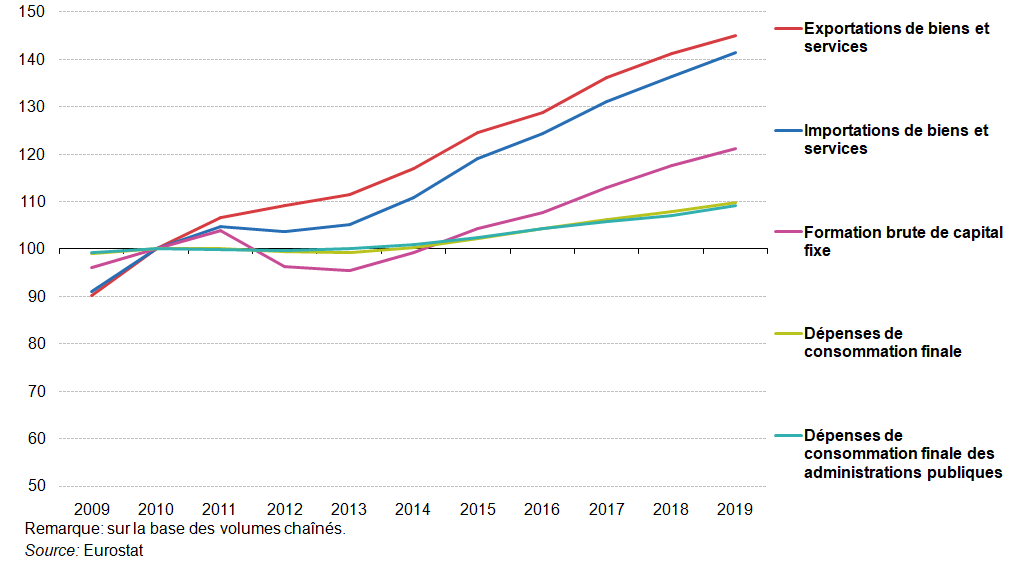
V – LA PERTE D’ADDITIVITÉ
Les prix chaînés posent en revanche certains problèmes. En effet, avec le chaînage, les séries perdent la propriété d’additivité stricte [8]. Il en résulte que, d’une part, les égalités comptables ne sont pas strictement respectées sur des données en volume chaînées, et que, d’autre part, les séries chaînées correspondant à des niveaux plus agrégés ne sont pas égales à la somme des séries de niveau plus fin chaînées qui composent ce niveau agrégé (voir tableau ci dessous). En outre, des problèmes techniques supplémentaires ont conduit les comptables nationaux à proposer une méthode spécifique pour produire des séries de variations de stocks en volume chaînées..
Malgré tout, les volumes et les prix en comptabilité nationale restent calculées selon la méthode du chaînage pour deux raisons principales.
Tout d’abord, avec des indices chaînés, les taux de croissance ne dépendent pas de la date de référence et ne sont pas révisés en cas de modification de cette date de référence dans le cadre notamment d’un changement de base.
Par ailleurs, les volumes aux prix de l’année précédente chaînés offrent l’avantage de prendre en compte la déformation des prix relatifs, ce qui est particulièrement souhaitable lorsque les prix de certains produits évoluent de façon très différente entre eux. Les pondérations sont actualisées tout au long de la série, ce qui permet a priori de tenir compte de l’évolution de la structure de l’économie et de limiter les biais de substitution. En ce sens, ce mode de présentation des chiffres permet ainsi de fournir aux utilisateurs les séries les plus pertinentes possibles pour décrire l’évolution réelle de l’activité.
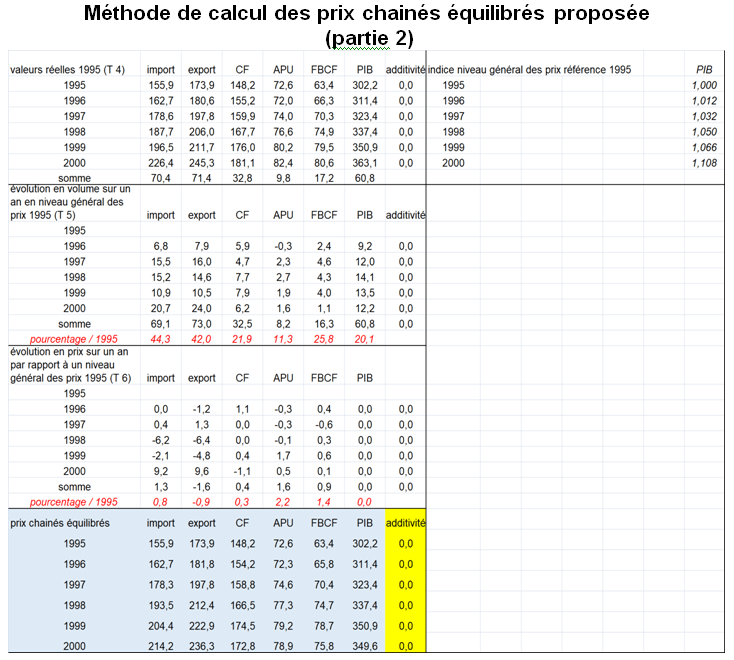
Séries chainés : chaînage de l’ensemble des niveaux élémentaires et chaînage de l’ensemble des agrégats (exemple fictif : pas d’égalité comptable mais une pondération chaque année)